Hopf fibration in Blender with add-ons

OverView

I read about Wikipedia's Hopf fibration¹ page. This graphic model is really beatiful. After some research, I found a blog https://nilesjohnson.net/hopf-production.html, offering mathematical details, a fibration animation in a Youtube Video² and source codes in his GitHub page³.

In this article, I tried to create the model in Blender⁴ with reference to the original SageMath⁵ source code.

Blender node add-ons

It is possible to write python codes in Blender, but this app also has some useful add-ons which offer us node editors. I'll use sverchok⁶ add-on and animation node⁷ in this entry.

Creating Hopf fibration with Blender add-ons

In the fibration video, this four types of rotation (in spherical coordinate) seems to be used.

• Great Circle
• Latitude
• Spiral
• Flower

I'll write some scripts for these types. Though calculus (differentiation and integration) is used to arrange vertices evenly for spiral and flower in the original source, I'll skip this to avoid writing complex codes.

Hopf fibration with sverchok

I'll make the fibration following this procedure.

• Write scripts and load them in 'Script Node Lite' nodes.
• Make splines from vertices these scripts generated with 'Polyline Viewer' node
• Convert them to meshes with 'Object ID Mk2' and 'BMesh Viewer'
• Add vertex colors to the outputs with colors from original vertices.

Scripts

These are the scripts to generate vertices on a sphere.

• hopf_fibration_greatcircle_sv.py

"""
in init_pos v d=(1,0,1.570796) n=2
in final_pos v d=(1,0,0) n=2
in division s d=10 n=2
out verts v
"""

import math
import numpy as np

verts = [[]]
v = []
p = np.array([init_pos[0]*math.cos(init_pos[1])*math.sin(init_pos[2]), init_pos[0]*math.sin(init_pos[1])*math.sin(init_pos[2]), init_pos[0]*math.cos(init_pos[2])])
q = np.array([final_pos[0]*math.cos(final_pos[1])*math.sin(final_pos[2]), final_pos[0]*math.sin(final_pos[1])*math.sin(final_pos[2]), final_pos[0]*math.cos(final_pos[2])])

a = np.dot(p, q)
w = q - a*p
q_prime = w/np.linalg.norm(w)
alpha = 2*math.pi

for i in range(division):
    alpha_i = alpha*i/division
    v_np = p*math.cos(alpha_i)+q_prime*math.sin(alpha_i)
    v.append(tuple(v_np))
    # v.append((r, phi, theta))
verts[0] = v

• hopf_fibration_latitude_sv.py

"""
in init_pos s d=0.0 n=2
in final_pos s d=1.5708 n=2
in polar s d=1.5708 n=2
in division s d=10 n=2
out verts v
"""

import math

p = init_pos
q = final_pos

verts = [[]]
v = []
for i in range(division):
    r = 1
    az = p + (i/division) * (q - p)
    v.append((r*math.cos(az)*math.sin(polar), r*math.sin(az)*math.sin(polar), r*math.cos(polar)))
    # v.append((r, phi, theta))
verts[0] = v

• hopf_fibration_spiral_sv.py

"""
in init_pos v d=(1,0,1.570796) n=2
in final_pos v d=(1,3.141592,0) n=2
in division s d=32 n=2
out verts v
"""

import math
import numpy as np

verts = [[]]
v = []

t_ = np.linspace(0.0, 1.0, division)
az_start = init_pos[1]
po_start = init_pos[2]
az_end = final_pos[1]
po_end = final_pos[2]


for t in t_:
    az_t = (1-t)*az_start + t*az_end
    po_t = (1-t)*po_start + t*po_end
    v.append((math.cos(az_t)*math.sin(po_t), math.sin(az_t)*math.sin(po_t), math.cos(po_t)))
verts[0] = v

• hopf_fibration_flower_sv.py

"""
in N s d=4 n=2
in A s d=0.5 n=2
in B s d=0.44880 n=2
in P s d=1.570796 n=2
in Q s d=0.0 n=2
in division s d=32 n=2
out verts v
"""

# N = 4 #controls the number of petals
# A = .5 #controls the fattness of the petals
# B = -pi/7 #controls the amplitude of the polar angle range
# P = pi/2 #controls the latitude of the flower
# Q = 0 #shifts the azmuthal angle

import math
import numpy as np

verts = [[]]
v = []

t_ = np.linspace(0.0, 1.0, division)

for t in t_:
    az_t = (2*math.pi)*t + A*math.cos(N*(2*math.pi)*t) + Q
    po_t = B*math.sin(N*(2*math.pi)*t) + P
    v.append((math.cos(az_t)*math.sin(po_t), math.sin(az_t)*math.sin(po_t), math.cos(po_t)))
verts[0] = v

This script offers modified stereographic projection to the vertices.

• hopf_fibration_sv.py

"""
in verts_in v d=[] n=1
in num s d=10 n=2
out verts_out v
out edges_out s
"""

import numpy as np
import math

# total = len(verts_in)
# print(total)
verts_out = [] # *total
edges_out = [] # *total

for i, vert in enumerate(verts_in):
    a, b, c = vert[0], vert[1], vert[2]
    verts = []
    edge_set = set()
    if c >= 0.997:
        z_ = np.linspace(-1, 1, num)
        v = []
        for z in z_:
            v.append((0, 0, z))
        verts = v
    elif c == -1.:
        t_ = np.linspace(0, 2*math.pi, num)
        v = []
        for t in t_:
            v.append((0.5*math.cos(t), 0.5*math.sin(t), 0))
        verts = v
    else:
        alpha = math.sqrt(0.5 * (1 + c))
        beta = math.sqrt(0.5 * (1 - c))

        phi_ = np.linspace(0, 2*math.pi, num)
        v = []
        for phi in phi_:
            theta = math.atan2(a, b) - phi
            w, x, y, z = alpha * math.cos(theta), -1 * beta * math.cos(phi), -1 * beta * math.sin(phi), alpha * math.sin(theta)
            rr = math.acos(w) * (1./math.pi) * (1./math.sqrt(1-w**2))
            v.append((x*rr, y*rr, z*rr))
        verts = v
    
    verts_out.append(verts)
            
    for j in range(num-1):
        edge_set.add(tuple([j, j+1]))
    if c < 0.997:
        edge_set.add(tuple([num-1, 0]))
    edges_out.append(list(edge_set))

Node Trees and results

These are the node trees and results. To display vertex color on solid mode, select 'Vertex' color in Viewport Shading panel found in the top of the viewport.

• Great Circle

• Latitude

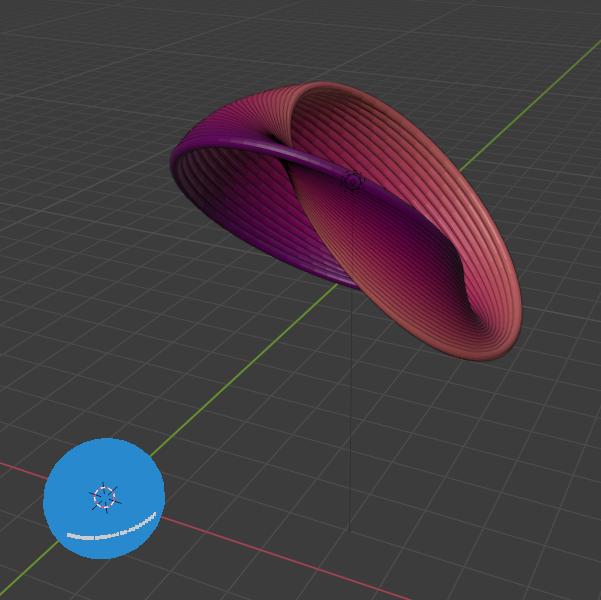
• Spiral

• Flower

Next one is generated with multiple latitude tree nodes.

• Multiple Latitude

These node trees can be imported from json files. I have uploaded them to my GitHub repository. https://github.com/asahidari/hopf_fibration_b3d

Hopf fibration with animation nodes

I'll make the fibration following this procedure.

• Write scripts and load them in 'Script' nodes.
• Make splines with 'Spline from Edges'.
• Convert them to meshes with Mesh from Spline'.
• Add vertex colors to the outputs with colors from original vertices, using 'Insert Vertex Color Layer' node, 'Set Vertex Color' node and etc.

Scripts

These are the scripts to generate vertices on a sphere.

• hopf_fibration_greatcircle_an.py

"""
in init_pos v d=(1,0,1.570796) n=2
in final_pos v d=(1,0,0) n=2
in division s d=10 n=2
out verts v
"""

import math
import numpy as np
from mathutils import Vector
from animation_nodes.data_structures import Vector3DList

verts = Vector3DList()
v = []
p = np.array([init_pos[0]*math.cos(init_pos[1])*math.sin(init_pos[2]), init_pos[0]*math.sin(init_pos[1])*math.sin(init_pos[2]), init_pos[0]*math.cos(init_pos[2])])
q = np.array([final_pos[0]*math.cos(final_pos[1])*math.sin(final_pos[2]), final_pos[0]*math.sin(final_pos[1])*math.sin(final_pos[2]), final_pos[0]*math.cos(final_pos[2])])

a = np.dot(p, q)
w = q - a*p
q_prime = w/np.linalg.norm(w)
alpha = 2*math.pi

for i in range(division):
    alpha_i = alpha*i/division
    v_np = p*math.cos(alpha_i)+q_prime*math.sin(alpha_i)
    v.append(Vector((v_np[0], v_np[1], v_np[2])))
    # v.append((r, phi, theta))
verts.extend(v)

• hopf_fibration_latitude_an.py

"""
in init_pos s d=0.0 n=2
in final_pos s d=1.5708 n=2
in polar s d=1.5708 n=2
in division s d=10 n=2
out verts v
"""

import math
from mathutils import Vector
from animation_nodes.data_structures import Vector3DList

p = init_pos
q = final_pos

verts = Vector3DList()
v = []
for i in range(division):
    r = 1.0
    az = p + (i/division) * (q - p)
    v.append(Vector((r*math.cos(az)*math.sin(polar), r*math.sin(az)*math.sin(polar), r*math.cos(polar))))
    # v.append((r, phi, theta))
verts.extend(v)

• hopf_fibration_spiral_an.py

"""
in init_pos v d=(1,0,1.570796) n=2
in final_pos v d=(1,3.141592,0) n=2
in division s d=32 n=2
out verts v
"""

import math
import numpy as np
from mathutils import Vector
from animation_nodes.data_structures import Vector3DList

verts = Vector3DList()
v = []

t_ = np.linspace(0.0, 1.0, division)
az_start = init_pos[1]
po_start = init_pos[2]
az_end = final_pos[1]
po_end = final_pos[2]


for t in t_:
    az_t = (1-t)*az_start + t*az_end
    po_t = (1-t)*po_start + t*po_end
    v.append(Vector((math.cos(az_t)*math.sin(po_t), math.sin(az_t)*math.sin(po_t), math.cos(po_t))))
verts.extend(v)

• hopf_fibration_flower_an.py

"""
in N s d=4 n=2
in A s d=0.5 n=2
in B s d=0.44880 n=2
in P s d=1.570796 n=2
in Q s d=0.0 n=2
in division s d=32 n=2
out verts v
"""

# N = 4 #controls the number of petals
# A = .5 #controls the fattness of the petals
# B = -pi/7 #controls the amplitude of the polar angle range
# P = pi/2 #controls the latitude of the flower
# Q = 0 #shifts the azmuthal angle

import math
import numpy as np
from mathutils import Vector
from animation_nodes.data_structures import Vector3DList

verts = Vector3DList()
v = []

t_ = np.linspace(0.0, 1.0, division)

for t in t_:
    az_t = (2*math.pi)*t + A*math.cos(N*(2*math.pi)*t) + Q
    po_t = B*math.sin(N*(2*math.pi)*t) + P
    v.append(Vector((math.cos(az_t)*math.sin(po_t), math.sin(az_t)*math.sin(po_t), math.cos(po_t))))
verts.extend(v)

This script offers modified stereographic projection to the vertices.

• hopf_fibration_an.py

"""
in verts_in v d=[] n=1
in num s d=10 n=2
out verts_out v
out edges_out s
"""

import numpy as np
import math
from mathutils import Vector
from animation_nodes.data_structures import Vector3DList, EdgeIndicesList

# total = len(verts_in)
# print(total)
verts_out = Vector3DList() # *total
edges_out = EdgeIndicesList() # *total

a, b, c = vert_in[0], vert_in[1], vert_in[2]
verts = []
edge_set = set()
if c >= 0.997:
    z_ = np.linspace(-1, 1, num)
    v = []
    for z in z_:
        v.append(Vector((0, 0, z)))
    verts = v
elif c == -1.:
    t_ = np.linspace(0, 2*math.pi, num)
    v = []
    for t in t_:
        v.append(Vector((0.5*math.cos(t), 0.5*math.sin(t), 0)))
    verts = v
else:
    alpha = math.sqrt(0.5 * (1 + c))
    beta = math.sqrt(0.5 * (1 - c))

    phi_ = np.linspace(0, 2*math.pi, num)
    v = []
    for phi in phi_:
        theta = math.atan2(a, b) - phi
        w, x, y, z = alpha * math.cos(theta), -1 * beta * math.cos(phi), -1 * beta * math.sin(phi), alpha * math.sin(theta)
        rr = math.acos(w) * (1./math.pi) * (1./math.sqrt(1-w**2))
        v.append(Vector((x*rr, y*rr, z*rr)))
    verts = v

verts_out.extend(verts)
        
for j in range(num-1):
    edge_set.add(tuple([j, j+1]))
if c < 0.997:
    edge_set.add(tuple([num-1, 0]))
edges_out.extend(list(edge_set))

Next image is 'Script' nodes with these scripts.

These scripts have been uploaded on my Github repository. https://github.com/asahidari/hopf_fibration_b3d

Subprograms

In animation nodes environment, to implement some loop functions, you need to use some 'Subprogram' nodes.

This loop generates meshes from splines and vertices on a sphere.

Next loop tree generates vertex colors from vertices on a sphere.

Next subprogram adds vertex colors to output objects (and meshes).

Sphere

This node make a sphere, on which spherical-coordinate vertices will be arranged.

Main Tree Nodes and results

These are the node trees and results.

• Great Circle
• Latitude
• Spiral
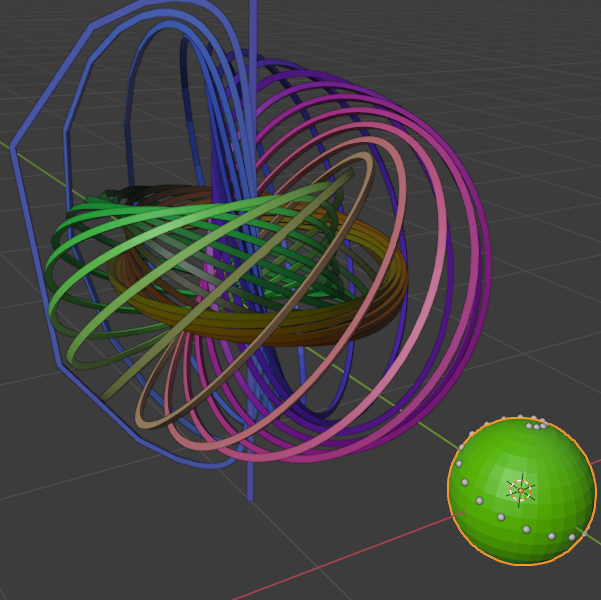
• Flower
• Multiple Latitudes

Environment

• Blender 2.83
• Sverchok 0.6
• Animation nodes 2.1.7

References:

• http://www.dimensions-math.org/Dim_CH7_JP.htm
• https://www.youtube.com/watch?v=AUV6NysrFj8
• https://www.youtube.com/watch?v=eqeqbjec97w

---

1. https://en.wikipedia.org/wiki/Hopf_fibration↩

2. https://www.youtube.com/watch?v=AKotMPGFJYk&feature=emb_title↩

3. https://github.com/nilesjohnson/hopf_fibration↩

4. https://www.blender.org↩

5. https://www.sagemath.org↩

6. https://github.com/nortikin/sverchok↩

7. https://animation-nodes.com/↩