Rigid Origami Folding in Blender with add-ons

f:id:asahidari:20200728133047p:plain

Updated (Aug 23, 2020)

This script node was already merged in sverchok's master. So you can use rigid origami node in sverchok (select modifier change -> rigid origami) without using this script node.

And when this node was merged, some socket interfaces has been changed.

object socket -> verts/edges/faces socket
valleys/mountains and valley/mountain angle -> fold edge indices/angles

To get the details, please visit the following pull request. https://github.com/nortikin/sverchok/pull/3416

Overview

Researches about origami are currently active in computer graphics field. Though there are still many restrictions, many patterns also can be folded. In this article, I wrote a script to be able to fold some origamis with Blender's add-on, sverchok, following some thesis about rigid origami folding.

Theory of Rigid Origami Folding

Though there are some informative articles about origami, I'll mainly follow an article of Rigid origami simulation¹. In the article, the main topic is kinematics of rigid origami. In the beginning, there is an explanation about edge angles around a single vertex. f:id:asahidari:20200728101343p:plain

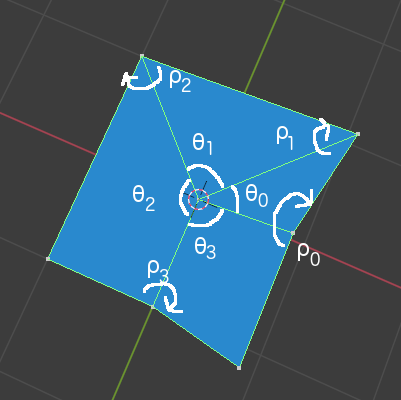
Around a vertex inside of a paper, rotation matrices satisfies following equations.

$Xi = \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & cos\rho_{i} & -sin\rho_{i} \\ 0 & sin\rho_{i} & cos\rho_{i} \end{array} \right) \left( \begin{array}{ccc} cos\theta_{i} & -sin\theta_{i} & 0 \\ sin\theta_{i} & cos\theta_{i} & 0\\ 0 & 0 & 1 \end{array} \right) \\$

$F = X_{1}X_{2}\cdots X_{i}\cdots X_{n} = I\\ \frac{\partial F}{\partial t} = \frac{\partial F}{\partial \rho_{1}} \dot{\rho_{1}} + \frac{\partial F}{\partial \rho_{2}} \dot{\rho_{2}} +\cdots \frac{\partial F}{\partial \rho_{i}} \dot{\rho_{i}} + \cdots \frac{\partial F}{\partial \rho_{n}} \dot{\rho_{n}} = \left( \begin{array}{ccc} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array} \right)$

Partial derivative of the constraint function is represented in the following form using independent a, b and c.

$\frac{\partial F}{\partial \rho_{i}} = \left( \begin{array}{ccc} 0 & -a & c \\ a & 0 & -b \\ -c & b & 0 \end{array} \right) \quad$

To get the delta rho angles of the edges, use the following equations with the each variables of a, b and c. And this is the single vertex version. To know the multiple vertices version, please read the original article.

$\frac{\partial F}{\partial \rho_{i}} = C \mathbf{\dot \rho} = \left( \begin{array}{ccc} a_{1} & \cdots & a_{n} \\ b_{1} & \cdots & b_{n} \\ c_{1} & \cdots & c_{n} \end{array} \right) \left( \begin{array}{ccc} \dot \rho_{1} \\ \dot \rho_{2} \\ \cdots \\ \dot \rho_{n} \end{array} \right) = \left( \begin{array}{ccc} 0 \\ 0 \\ 0 \end{array} \right) \\ \mathbf{\dot \rho} = \left[ I_{N} -C^{+} C\right] \mathbf{\dot \rho_{0}} \quad \left( C^{+} \, is \, the \, Moor-Penrose \, inverse \, of \, C, \\ \rho_{0} \, is \, the \, unconstrained \, value \, of \, the \, angles \, velocity \right)$

Implementation

I uploaded the code to my GitHub page. This code can be used in sverchok's SNLite script node. https://github.com/asahidari/rigid_origami_folding_b3d

How to use it

sverchok

After download the script file, open it in text editor inside Blender. After that, you can load the script into the sverchok's script node. f:id:asahidari:20200728134118p:plain

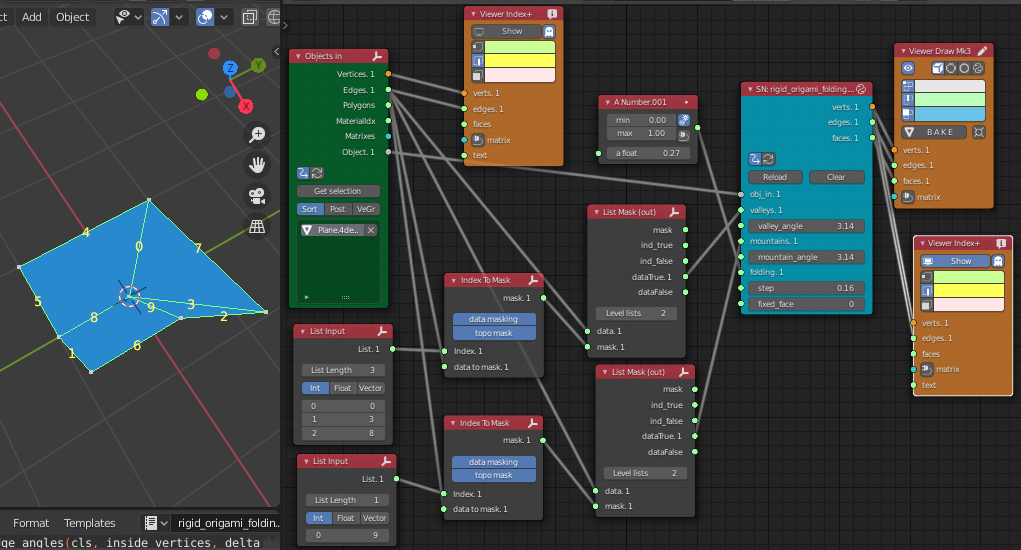
This is the image of the script node. f:id:asahidari:20200728134210p:plain Parameters:

obj_in: paper object which has some edges inside
valleys: valley fold edge list
valley_angle: angle (radian) of valley edges
mountains: mountain fold edge list
mountain_angle: angle (radian) of mountain edges
folding: ratio of the folding angle (0 to 1)
step: delta rho angle step (for example, pi * 0.005, pi * 0.01, pi * 1.0)
fixed_face: index number of fixed face

Next image is an example of usage. f:id:asahidari:20200728134229p:plain

Animation Nodes

(constructing)

Limitations

This code is not yet merged in sverchok (July 2020).
As the original article says, some crease patterns may not be folded appropriately.
It may be difficult to find where error occurs when there are something wrong. I wish these points would help you to solve the problems.
- Confirm that all edges inside of the paper are used as valleys or mountains.
- Avoid including peripheral edges (Probably nothing wrong happen, but it may confuse you).
- Check if some valley edges were wrongly included in mountains (and vice versa).
- When the result is none or slightly move, try to change the 'step' parameter (math.pi * (0.001 ~ 1.0)) This may sometimes goes well.
- To find foldable origami fold patterns, try to search for images with the words like "crease lines origami".