Creating Riemann's Minimal Surface 3D model in python

Overview
When Searching for Riemann's minimal surface, you can find many drawings generated in Mathematica. But it seems difficult to find the way to create the surface in another environments. So I tried to make another example,using python. (Octave or MATLAB may be possible to do the same thing.)
Parametric equations for the Riemann's Minimal Surface
I found an article about parametric equations to generate a fundamental piece of the surface, the title of the writing is 'The Riemann Minumal Examples'*1. In this document, mathematical equations and functions to calculate X,Y,Z values of the surface are written in chapter 4.2.1 'Parametarizing the surface with Mathematica'.
Using sympy's elliptic integral functions
In the document, you will find elliptic integral functions (ellipticF, ellipticE) to get X, Y, Z values. In python, 'sympy'*2 has the functions(elliptic_f, elliptic_e), and it also offers plotting views(, using matplotlib as a backend).
Creating a fundamental piece of Riemann's minimal surface
Following the paper, I wrote the functions in python.
After defining the equations, 3d plotting shows the piece in a graph view.
The result is this.

Rotating the piece around the center axis
After getting the fundamental piece, rotate it around the center axis and mirror it on the X or Y axis, to generate one 'step' of 'staircase' of the surface.
(To show the rotation-axis with the surface, I add a cross line to view the whole parts.)
Then, plot them.
However, it requires long time to calculate and show all the results. So if you want to get the 'step' in short time, After exporting one or two pieces into STL files, rotate and mirror them by using other 3d softwares. Next image displays two pieces imoprted in Blender.
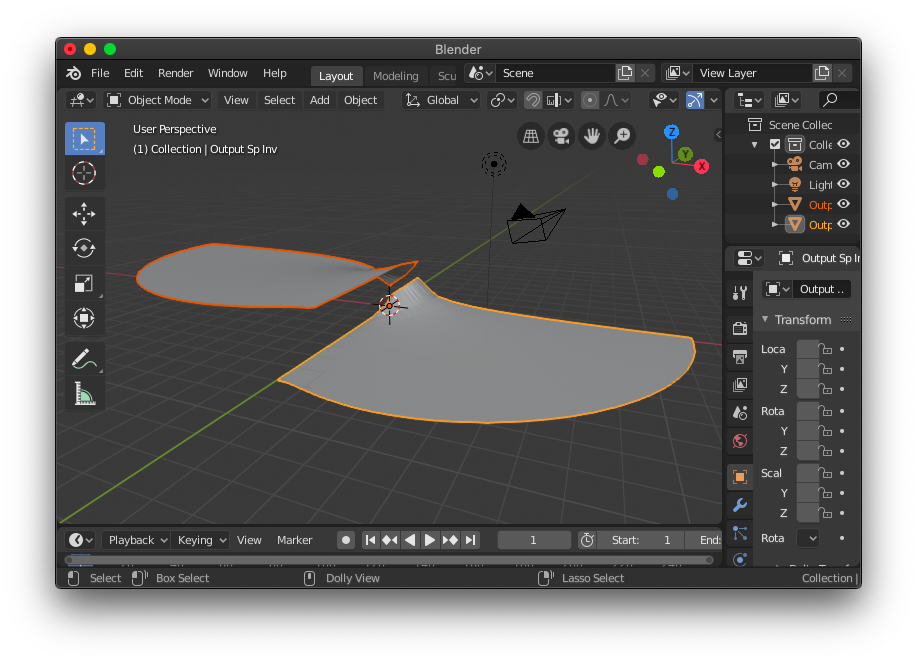
Convert sympy symbols to numpy arrays
To export the 3d surface in STL format, you need to convert the sympy symbols to numpy arrays.
In this code, the symbols functions are once lambdified with 'mpmath' mode, and then changed to float arrays with fromnumpyfunc function. Because in 'numpy' mode, 'elliptic_f' and 'elliptic_e' functions cannot be recognized properly.
Before exporting the surface, I noted down about 'e' parameter.
Adjust 'e' parameters to modify the shape
In the first code, I assigned '0.01' to a parameter 'e' instead of default value '0.1' in the original article. Because when I use '0.1' to 'e', the inner circle is halved and opend, and the result makes it difficult to connect the original piece with the rotated one around the 'neck' part. (I'm not so familiar with elliptic integral functions, so please tell me if you know better options. ) Next code shows the difference.
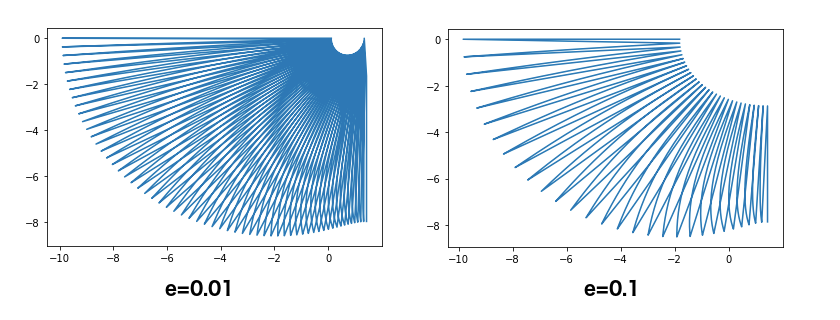
Exporting to a STL file
After getting the surface graph, you can export the pieces into STL files by using surf2stl-python*3. (Probably, you can also get them by using numpy-stl*4.) This script triangulate the mesh. If you want quadified mesh, you can do it by using other 3d software tools. (For example, Blender offers the way to select Menu->Faces->Tri to Quad in Edit mode).
In this article, I exported the original piece and a rotated one.
After some modifications (connecting the 'neck' parts, mirroring the connected one, copying the 'step', subdividing the surface, etc.), you'll get the 3d mesh of the Riemann's minimal surface. Here is the example in Blender.
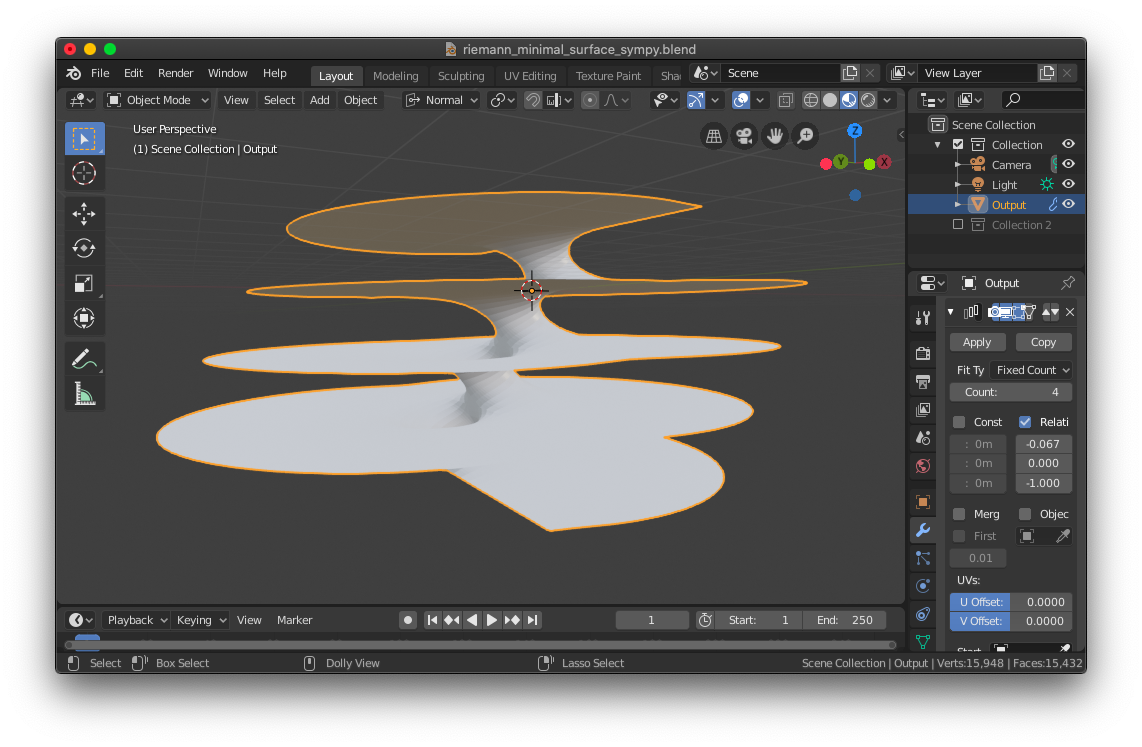
This modeling process is uploaded to github gist.
https://gist.github.com/asahidari/0a4782827cb34412a7638395c46480d2
References
* The Riemann Minumal Examples
http://wpd.ugr.es/~jperez/wordpress/wp-content/uploads/14-.pdf
* Sympy Plotting
https://docs.sympy.org/latest/modules/plotting.html
Environment
* Python 3
* Sympy
* Numpy
* Matplotlib
* Blender 2.8